
This paper explores, theoretically and empirically, the role of the declining gender gap in education in the demographic transition and the emergence of modern economic growth. Specifically, the paper develops a model in the tradition of the unified growth theory that captures and interconnects the key empirical features of the demographic transition, the decline in gender gap in education, and the transition to sustained growth across less-developed economies. The mechanism on which the model relies comprises several interplaying components. First, technological progress reduces housework time through the creation and diffusion of labor-saving home appliances, which frees women’s time for childrearing, resulting in an initial increase in fertility, as well as in labor-force participation. Second, due to the possibly higher female labor-force participation as housework time decreases, households invest relatively more in their daughters’ education, given its higher return following the initial imbalance. This improves gender equality in education and increases the opportunity cost of childrearing, which leads to a subsequent decrease in fertility. Third and finally, the decrease in the education gender gap through higher investment in daughters’ education increases average human capital, thus accelerating technological progress in turn. This reinforcing loop results in the transition to a new fertility regime and accelerated economic growth. We provide the empirical confirmation of the model’s predictions using data from developing countries in the late 20th and early 21st centuries.
This is a preview of subscription content, log in via an institution to check access.
Price includes VAT (France)
Instant access to the full article PDF.
Rent this article via DeepDyve
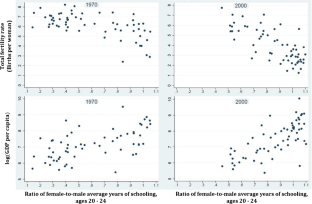
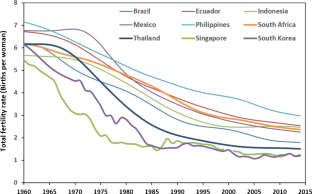
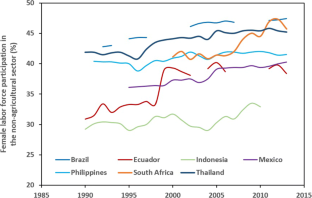
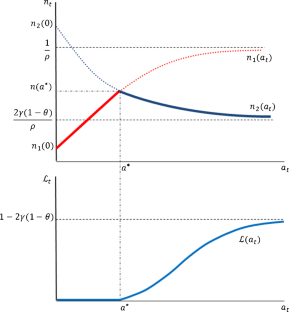



A demographic transition refers to the passing from a high fertility and high mortality regime—including child mortality—to a low fertility and low mortality one, generating an inverted U-curve for net fertility along the way. For exposition purposes, we do not address mortality throughout the paper, but fertility here can be interpreted as net fertility. Child mortality can be included in the model without changing its results significantly. This is consistent with the related literature, where the term demographic transition is used instead of fertility transition to refer implicitly to the potential extension/power of the models. In addition, as pointed out in Herzer et al. (2012), the decline in fertility triggered by falling mortality is not essential to explain the secular decline in population growth experienced in the 20th century. For a more comprehensive discussion on this, see Doepke (2005) and Galor (2012).
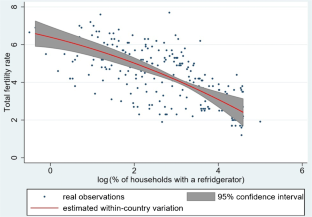
The share of households in Bangkok with refrigerators increased from 26 to 62%, and from 63 to 95% in Taiwan in the period 1975–1984. The generalization of home appliances also shows up in the increase in residential electricity consumption per capita, from 17 to 110 kWh per capita in the period 1970–1986 in Thailand; from 25 to 248 kWh in South Korea; from 75 to 190 kWh in Mexico; and from 90 to 261 kWh in Brazil (Mayers and Sathaye 1989). The impact of technological progress on the economic role of women was even anticipated very early in the 20th century, as shown by Thomas A. Edison’s words: “The housewife of the future will be neither a slave to servants nor herself a drudge. She will give less attention to the home, because the home will need less, she will be rather a domestic engineer than a domestic laborer, with the greatest of all handmaidens, electricity, at her service. This and other mechanical forces will so revolutionize the woman’s world that a large portion of the aggregate of woman’s energy will be conserved for use in broader, more constructive fields,” Good Housekeeping Magazine, LV, no. 4 (October 1912, p. 436). Quoted in Greenwood et al. (2005a).
Recently, Bucci and Prettner (2020) also advance an endogenous growth model to consider the relationship between innovation and demographic change. However, different from ours, Bucci and Prettner (2020) focus on the impact of population growth, through its effects on aggregate human capital accumulation, on research and development activities in production sectors (not in household sector) to account for the reversal between fertiltiy and innovation-driven productivity growth. In addition, Bucci and Prettner (2020) do not consider the gender dimension of the problem while it is the main focus of our paper.
Other factors such as the increase of income per capita (Becker 1960, Becker and Lewis 1973), the decrease of infant and child mortality (Kalemli-Ozcan 2002, 2003; Tamura 2006; Tamura et al. 2016; Tamura and Simon 2017), and the old-age security (Neher 1971; Caldwell 1976; Boldrin and Jones 2002) have been showed to be inconsistent, on their own, with the data, and therefore are considered as reinforcing minor factors rather than main factors in explaining the demographic transition. For a more comprehensive overview, see Galor (2011).
Using US data at county level, Bailey and Collins (2011) have identified a negative coefficient of the home technology adoption rate on fertility, while a baby boom implies a positive one. This result is usually interpreted as evidence contradicting Greenwood et al. (2005b). But in a paper reply to these finding, Greenwood et al. (2015) point to a misinterpretation by Bailey and Collins (2011), who ignore that poorer households adopted electricity and home appliances later than richer ones, while the latter intrinsically have lower fertility rates.
On women’s rights and marital bargaining power see also Basu (2006), Fernandez (2009), Doepke et al. (2012); Doepke and Tertilt (2019).
Specially in developing economies, conventions still make women responsible for childrearing and housework, while the labor market for mostly physically demanding tasks leads households to specialize in a division of labor that sees almost only men participating in wage labor. In Galor and Weil (1996), the opportunity cost of raising children is higher for men than women. Thus, the woman takes care of children until her time constraint is binding, when the man gets involved. However, Galor and Weil (1996) restrict the weight of children in preferences so that men do not participate in childrearing, devoting instead all their time to wage labor. Anyway, letting men do housework and childcare does not change the qualitative analysis as long as it is assumed they do less than women, which seems uncontroversial.
Greenwood et al. (2005a) argue that technological progress plays a key role in households’ allocation of time. Indeed, the appearance of a mass market for ready made clothes (in the 19th century) and the generalization of appliances—washing machines, vacuum cleaners, refrigerators (in the mid-20th century), etc.—as well as frozen foods and ready meals (in the mid-late 20th century) freed a considerable amount of time from housework.
This effect, that would indeed foster fertility, can be introduced without changing the qualitative results, in particular, the explanation of the hump-shaped fertility pattern. On the increasing part of the hump, this effect reinforces our mechanism, while on the decreasing part it is dominated by the reduction in fertility through an increased gender equality in education—for reasonable parameters and functional forms.
We assume that the gender birth ratio (male over female) is 1 which is close to the natural gender ratio. Accordingly, a “household-child” is assumed to consist of a son and a daughter.
The main results of our model do not change if we assume that the input for education investment is parents’ time instead of income, while this alternative modeling choice requires additional assumptions about who—the father or the mother—is responsible for it, or what is the parents’ division of labor in educating children. At any rate, regardless of this, the education investments in our model would correspond, in the alternative approach, to the opportunity cost of educating children. All in all, the gender gap in education and its properties are determined by Eqs. (11) and (12) whose qualitative behavior does not depend on this modeling choice. Ours is, at any rate, in accordance with the fact that the importance of formal education for the labor market increasingly exceeds that of education involving parents’ time.
Indeed, ϕt+ 1 has been assumed to be determined by the level of technology at+ 1, which itself is determined by the education investments et and \(\tilde _\) chosen for this household by its parent household (see Eq. (13) below), all of which is known to it.
That is to say, a daughter’s education has a value for her parents, independently of the use that she makes of it. This is consistent with Becker and Tomes (1979) and Galor and Weil (2000), and captures other aspects excluded from the model, like the use of education as hedging device against the risk of a daughter’s divorce: see Chiappori and Weiss (2007).
This necessarily requires the condition \(1-\left [\frac <\gamma (1-\theta )><1-\gamma (1-\theta )>\right ]^>0\) —since ϕ is decreasing and non-negative for all a—i.e., γ(1 − θ) < 1/2 must holds. This last condition obviously holds for an altruism factor γ < 1/2, conventionally assumed in the literature: e.g., Galor and Weil (1996), Doepke (2004), and Lagerlöf (2003, 2006). We will restrict the value of θ in such a way that this condition holds.
For the sake of simplicity, we do not take into account physical capital. However, the main results are robust when introducing physical capital and assuming diminishing returns for all production factors. Indeed, with physical capital and 3-period living households working and saving in the second period and consuming in the third—the first period being childhood—savings are lent to firms and their return is consumed in the third period, while education investments and fertility choices remain the same. Also, we ignore consumption when young. Nonetheless, with a log-linear utility the saving rate is constant and fertility is independent of the interest rate, and consumption when young could be incorporated into the logarithm utility function, altering the dynamics of the model by just a multiplicative constant.
The impact of human capital on technological progress might depend on the effective participation of workers in production, so that g would depend on \(\frac (e_^+[1-\phi (a_)-\rho n_]\tilde _^)\) instead. This would only slow down the transition to sustained growth, but not change it qualitatively (the proof is available upon request). It can nonetheless be argued that women’s human capital impacts technological progress through childrearing via the children’s cognitive abilities, capacity of adaptation to new knowledge, and health, which in turn impact their human capital. The function g(.) describing the dynamics for technology follows the literature of unified growth theory, e.g., Galor and Weil (2000), Galor and Moav (2002), Diebolt and Perrin (2013a, b).
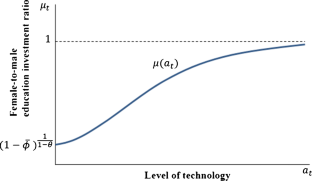
In Section 5 and in the Appendix we introduce heterogeneity across genders in non-cognitive skills to generate a reversal of this bias in education investment.
Lemma 1 is also consistent with the empirical results in Klasen (2002) showing a positive effect of gender equality in education on economic growth. Klasen (2002) shows that gender inequality in education affects economic growth directly by lowering the average level of human capital, and indirectly through its impact on population and investment.
This is just a sufficient condition to guarantee fertility decreasing with technological progress when the level of technology is high enough.
Some studies in the literature provide empirical evidence on the positive correlation between income/productivity and fertility in early stages of development supporting this Malthusian feature (see Crafts and Mills (2009) for England in the 16th–18th centuries, Lagerlöf (2015) for Sweden in the 18th–19th centuries, and Ashraf and Galor (2011) for the period 1–1500 CE). Several theories also predict such a positive correlation in early stages of development (see, e.g., Malthus 1798; Galor and Weil 2000, Galor and Moav 2002).
The model abstracts from child mortality to explain the demographic transition. Indeed, there has been a lack of consensus in the literature about the role of child mortality in explaining demographic transition. Kalemli-Ozcan (2002, 2003), Tamura (2006), Tamura et al. (2016), Tamura and Simon (2017), and recently Cuberes and Tamura (2019) are in favor of the view that falls in child mortality may induce declines in fertility. Using the altruistic parents model of Barro and Becker (1989), Doepke (2005) provides results suggesting that the fall in net fertility during the 19th century in the industrialized countries was driven by factors other than the fall in child mortality, pointing out that the decline in child mortality has been dismissed as a cause of the decline in fertility, because of the inconsistency of this link. Galor (2012) shares this view, showing that the fall in fertility in Western Europe started nearly a century after the decline in child mortality. Herzer et al. (2012) show a positive correlation between child mortality and fertility in the 20th century, but not a strong enough relationship to explain the secular decline of population growth. Murphy (2015) has shown empirically that child mortality had no impact on fertility during the demographic transition in France, while female education seems to have played a role. Recently, Blanc (2019) provides an interesting discussion on the determinants of the demographic transition in France.
Households anticipate the large fraction of time that daughters will have to devote to housework, due to the low level of technology. Since men’s supply of labor to the market is inelastic, while women have to spend a fraction of their time for housework, households allocate most of their education investment to their sons, making the education of their offspring very unequal across genders.
An incomplete list includes, to name but a few: the cost of college education (Goldin et al. 2006 and Becker et al. 2010a, b), the rise of divorce rates (Goldin et al. 2006and Chiappori et al. 2009), discrimination in labor market (Gosling 2003; Chiappori et al. 2009; Hazan and Zoabi 2015b), technological progress in the household sector (Chiappori et al. 2009), a short supply of men in the marriage market (Iyigun and Walsh 2007), differences in the anticipated dispersion of future wages across genders (Charles and Luoh 2003), and the independence of fertility on the gender composition of the children when the return to human capital is sufficiently high (Hazan and Zoabi 2015b).
List of dropped countries: Advanced countries (GDP per capita in PPP higher than 30,000 USD in 2017): Australia, Austria, Belgium, Canada, Czech Republic, Finland, Denmark, Estonia, France, Germany, Iceland, Israel, Ireland, Italy, Japan, Lithuania, Luxembourg, Netherlands, New Zealand, Norway, Portugal, Slovakia, Slovenia, South Korea, Spain, Sweden, Switzerland, UK, USA; Fiscal paradises, oil exporting Arab countries, and very small countries: American Samoa, Andorra, Aruba, Bahamas, Bahrain, Bermuda, British Virgin Islands, Brunei Darussalam, Channel Islands, Cayman Islands, Cyprus, Faroe Islands, Gibraltar, Guam, Greenland, Hong Kong, Isle of Man, Kuwait, Liechtenstein, Macao, Malta, Marshall Islands, Monaco, Nauru, Northern Mariana Islands, Oman, Palau, Panama, Qatar, San Marino, Saudi Arabia, Singapore, St. Martin (French part), Trinidad and Tobago, Turks and Caicos Islands, Tuvalu, United Arab Emirates, Virgin Islands (U.S.). We also run alternative specifications which: (1) focus only on countries and time periods for which GDP per capita is smaller than 20,000 (constant 2010 USD); (2) exclude only the advanced countries listed in footnote 24; and (3) exclude only the fiscal paradises, oil exporting Arab countries and very small listed in footnote 24. The results are consistent with those presented in this section. Results are available on request.
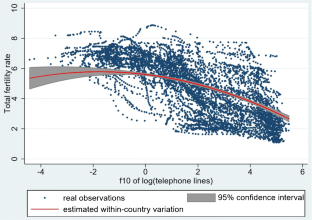
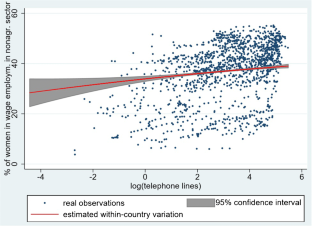
Our theory works with an overlapping generations model in which each period lasts for 20 - 25 years, corresponding to the reproductive period of women or childhood period of children. Consistent with our theory, the proxy for technological progress should cover a certain period of time, and not only a point in time when we observe fertility. That is to say, fertility observed in year 1970 should not only depend on the contemporary diffusion of home appliances but also on the expected diffusion of home appliances in the following years. Given the time delay between the penetration of time-saving home appliances and the penetration of telephone lines, we choose a 10-year forward gap for the variable ‘telephone lines’ when estimating its correlation with fertility. Results are robust when using a 5-year and a 15-year forward gap instead of the 10-year forward gap. Results are available on request.
The inverse U-shape is confirmed when using a reduced panel with observations until the year 1990 only. This robustness check was applied due to the fact that since the 1990s, telephone lines and other home appliances appear almost simultaneously in households.
Countries that are associated with the mentioned percentiles in our data set are for example: Benin in 1960 (second percentile), Tanzania in 1975 (sixth percentile), Hungary in 1980 (50th percentile) and Armenia in 1990 (66th percentile).
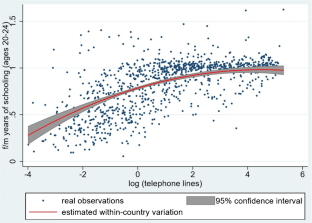
We also tested for the indirect link that exists between telephone density and fertility due to the relative increase in female education. We therefore first estimated the ratio of female to male education as a function of telephone density (while controlling for population density and child mortality), and then estimated fertility in a second step, as a function of the estimated gender ratio in education, while we include population density and child mortality as control variables. Our results suggest that an access of parents to time-saving home appliances leads to relative increases in their daughters’ education, which later on leads to decreases in TFRs within developing and emerging countries. Subsequent impacts are taken into account by allowing for a certain time delay between the observed technology level, the education and the fertility outcomes. Results are available upon request.
Note that, what we observe from the data is the reversal in education achievement— \(e_^\) and \(\tilde <\psi >\tilde ^\) for sons and daughters respectively—rather than education investment. Assumption 1 and \(\tilde <\psi >>1\) are sufficient for a reversal in education investment across genders, i.e., \(\underset <\lim >\tilde <\mu >(a)=\underset <\lim >\left [(1-\phi (a))\tilde <\psi >\right ]^>=\tilde <\psi >^>>1\) . Such a reversal, however, can occur for the education achievement even if there is not any in education investment, i.e., when \(\underset <\lim >\left [(1-\phi (a))\tilde <\psi >\right ]^>=1\) . Indeed, as proved in Proposition 2, \(e=\underset <\lim >e_=\underset <\lim >\tilde _=\tilde \) . As a consequence, eventually \(e^\tilde ^\) , so that the education achievement of the daughter exceeds that of the son even if the daughter’s education investment does not. That is to say, when the level of technology is sufficiently high the education achievement will reverse across genders because of both (i) the improvement in gender equality in education investment and (ii) the better efficiency of female education investment.
We thank the editors of the journal (Oded Galor and Madeline Zavodny), and four anonymous referees for providing helpful comments and suggestions. We also thank David de la Croix, Cuong Le Van, Sascha O. Becker, and David N. Weil for helpful discussions and encouragements. Earlier versions of this paper were presented at several seminars and conferences at the Universite catholique de Louvain, MCC Berlin, Vienna Institute of Advanced Studies, Catholic University of Lisbon, University of Warwick, University of Göttingen, and Osaka University. We have benefited from the comments and suggestions of participants. The scientific responsibility is ours.
This work received funding from an MIS Ulysse research grant from the Belgian F.R.S.-FNRS (Grant number F. 6007.09). The first author received support from the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant-in-Aid for Scientific Research JP15H05728.